Sistemas Lineares
Classificação de um sistema quanto ao número de soluções
Resolvendo o sistema 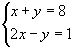 , encontramos uma única solução: o par ordenado (3,5). Assim, dizemos que o sistema é possível (tem solução) e determinado (solução única).
, encontramos uma única solução: o par ordenado (3,5). Assim, dizemos que o sistema é possível (tem solução) e determinado (solução única).
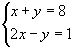 , encontramos uma única solução: o par ordenado (3,5). Assim, dizemos que o sistema é possível (tem solução) e determinado (solução única).
, encontramos uma única solução: o par ordenado (3,5). Assim, dizemos que o sistema é possível (tem solução) e determinado (solução única).
No caso do sistema 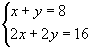 , verificamos que os pares ordenados (0,8), (1,7),(2,6),(3,5),(4,4),(5,3),...são algumas de suas infinitas soluções. Por isso, dizemos que o sistema é possível (tem solução) e indeterminado (infinitas soluções).
, verificamos que os pares ordenados (0,8), (1,7),(2,6),(3,5),(4,4),(5,3),...são algumas de suas infinitas soluções. Por isso, dizemos que o sistema é possível (tem solução) e indeterminado (infinitas soluções).
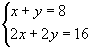 , verificamos que os pares ordenados (0,8), (1,7),(2,6),(3,5),(4,4),(5,3),...são algumas de suas infinitas soluções. Por isso, dizemos que o sistema é possível (tem solução) e indeterminado (infinitas soluções).
, verificamos que os pares ordenados (0,8), (1,7),(2,6),(3,5),(4,4),(5,3),...são algumas de suas infinitas soluções. Por isso, dizemos que o sistema é possível (tem solução) e indeterminado (infinitas soluções).
Para 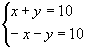 , verificamos que nenhum par ordenado satisfaz simultaneamente as equações. Portanto, o sistema é impossível (não tem solução).
, verificamos que nenhum par ordenado satisfaz simultaneamente as equações. Portanto, o sistema é impossível (não tem solução).
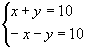 , verificamos que nenhum par ordenado satisfaz simultaneamente as equações. Portanto, o sistema é impossível (não tem solução).
, verificamos que nenhum par ordenado satisfaz simultaneamente as equações. Portanto, o sistema é impossível (não tem solução).Resumindo, um sistema linear pode ser:
a) possível e determinado (solução única);
b) possível e indeterminado (infinitas soluções);
c) impossível (não tem solução).
b) possível e indeterminado (infinitas soluções);
c) impossível (não tem solução).
Sistema normal
Um sistema é normal quando tem o mesmo número de equações (m) e de incógnitas (n) e o determinante da matriz incompleta associada ao sistema é diferente de zero.
Se m=n e det A 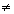 0, então o sistema é normal.
0, então o sistema é normal.
Regra de Cramer
Todo sistema normal tem uma única solução dada por:
em que i 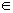 { 1,2,3,...,n}, D= det A é o determinante da matriz incompleta associada ao sistema, e Dxi é o determinante obtido pela substituição, na matriz incompleta, da coluna i pela coluna formada pelos termos independentes.
{ 1,2,3,...,n}, D= det A é o determinante da matriz incompleta associada ao sistema, e Dxi é o determinante obtido pela substituição, na matriz incompleta, da coluna i pela coluna formada pelos termos independentes.
Discussão de um sistema linear
Se um sistema linear tem n equações e n incógnitas, ele pode ser:
a) possível e determinado, se D=det A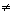 0; caso em que a solução é única.
0; caso em que a solução é única.
Exemplo:
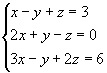
m=n=3
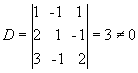
Então, o sistema é possível e determinado, tendo solução única.
b) possível e indeterminado, se D= Dx1 = Dx2 = Dx3 = ... = Dxn= 0, para n=2. Se n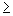 3, essa condição só será válida se não houver equações com coeficientes das incógnitas respectivamente proporcionais e termos independentes não-proporcionais.
3, essa condição só será válida se não houver equações com coeficientes das incógnitas respectivamente proporcionais e termos independentes não-proporcionais.
Um sistema possível e indeterminado apresenta infinitas soluções.
Exemplo:
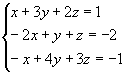
D=0, Dx =0, Dy=0 e Dz=0
Assim, o sistema é possível e indeterminado, tendo infinitas soluções.
c) impossível, se D=0 e 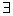 Dxi
Dxi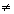 0, 1
0, 1 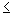 i
i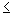 n; caso em que o sistema não tem solução.
n; caso em que o sistema não tem solução.
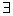 Dxi
Dxi
Exemplo:
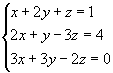
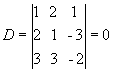
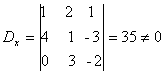
Como D=0 e Dx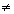 0, o sistema é impossível e não apresenta solução.
0, o sistema é impossível e não apresenta solução.
Sistemas Equivalentes
Dois sistemas são equivalentes quando possuem o mesmo conjunto solução.
Por exemplo, dados os sistemas:
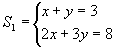 e
e 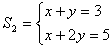
verificamos que o par ordenado (x, y) = (1, 2) satisfaz ambos e é único. Logo, S1 e S2 são equivalentes: S1 ~ S2.
Propriedades
a) Trocando de posição as equações de um sistema, obtemos outro sistema equivalente.
Por exemplo:
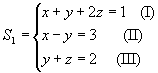 e
e 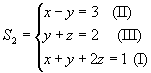
S1 ~S2
b) Multiplicando uma ou mais equações de um sistema por um número K (K

S1 ~S2
c) Adicionando a uma das equações de um sistema o produto de outra equação desse mesmo sistema por um número k ( K 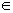 IR*), obtemos um sistema equivalente ao anterior.
IR*), obtemos um sistema equivalente ao anterior.
Por exemplo:
Dado 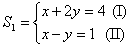 , substituindo a equação (II) pela soma do produto de (I) por -1 com (II), obtemos:
, substituindo a equação (II) pela soma do produto de (I) por -1 com (II), obtemos:
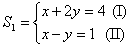 , substituindo a equação (II) pela soma do produto de (I) por -1 com (II), obtemos:
, substituindo a equação (II) pela soma do produto de (I) por -1 com (II), obtemos: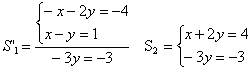
S1~S2, pois (x,y)=(2,1) é solução de ambos os sistemas.
Sistemas escalonados
Utilizamos a regra de Cramer para discutir e resolver sistemas lineares em que o número de equações (m) é igual ao número de incógnitas (n). Quando m e n são maiores que três, torna-se muito trabalhoso utilizar essa regra. Por isso, usamos a técnica do escalonamento, que facilita a discussão e resolução de quaisquer sistemas lineares.
Dizemos que um sistema, em que existe pelo menos um coeficiente não-nulo em cada equação, está escalonado se o número de coeficientes nulos antes do primeiro coeficiente não nulo aumenta de equação para equação.
Para escalonar um sistema adotamos o seguinte procedimento:
a) Fixamos como 1º equação uma das que possuem o coeficiente da 1º incógnita diferente de zero.
b) Utilizando as propriedades de sistemas equivalentes, anulamos todos os coeficientes da 1ª incógnita das demais equações.
c) Repetimos o processo com as demais incógnitas, até que o sistema se torne escalonado.
Vamos então aplicar a técnica do escalonamento, considerando dois tipos de sistema:
I. O número de equações é igual ao número de incógnitas (m=n)
Exemplo 1: 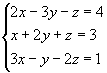
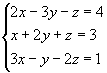
1ºpasso: Anulamos todos os coeficientes da 1º incógnita a partir da 2º equação, aplicando as propriedades dos sistemas equivalentes:
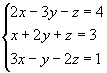 |
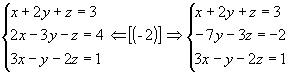 |
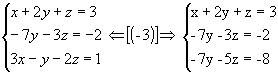 |
2º passo: Anulamos os coeficientes da 2º incógnita a partir da 3º equação:
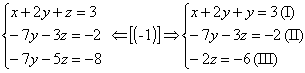 |
Agora o sistema está escalonado e podemos resolvê-lo.
-2z=-6  z=3
z=3
Substituindo z=3 em (II):
-7y - 3(3)= -2  -7y - 9 = -2
-7y - 9 = -2  y=-1
y=-1
Substituindo z=3 e y=-1 em (I):
x + 2(-1) + 3= 3  x=2
x=2
Então, x=2, y=-1 e z=3
Exemplo 2: 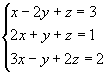
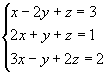
1º passo: Anulamos todos os coeficientes da 1º incógnita a partir da 2º equação:
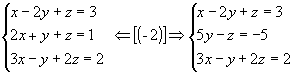 |
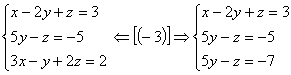 |
2º passo: Anulamos os coeficientes da 2ª incógnita, a partir da 3º equação:
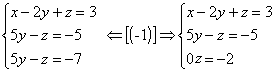 |
Dessa forma, o sistema está escalonando. Como não existe valor real de z tal que 0z=-2, o sistema é impossível.
II) O número de equações é menor que o número de incógnitas (m < n)
Exemplo: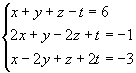
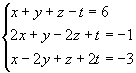
1º passo: Anulamos todos os coeficientes da 1º incógnita a partir da 2º equação:
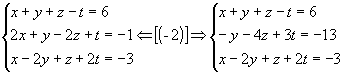 |
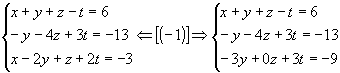 |
2º passo: Anulamos os coeficientes da 2º incógnita, a partir da 3º equação:
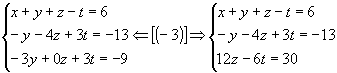 |
O sistema está escalonado. Como m<n, o sistema é possível e indeterminado, admitindo infinitas soluções. A diferença entre o número de incógnitas (n) e o de equações (m) de um sistema nessas condições é chamada grau de indeterminação (GI):
GI= n - m
Para resolver um sistema indeterminado, procedemos do seguinte modo:
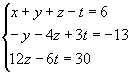 |
|
Como o grau de indeterminação é 1, atribuímos a uma das incógnitas um valor 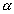 , supostamente conhecido, e resolvemos o sistema em função desse valor. Sendo t=
, supostamente conhecido, e resolvemos o sistema em função desse valor. Sendo t=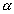 , substituindo esse valor na 3º equação, obtemos:
, substituindo esse valor na 3º equação, obtemos:
12z - 6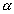 = 30
= 30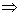 12z= 30 + 6
12z= 30 + 6
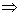
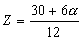 =
=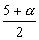
Conhecidos z e t, substituímos esses valores na 2º equação:
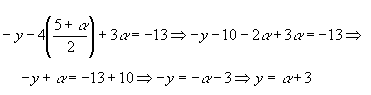
Conhecidos z,t e y, substituímos esses valores na 1º equação:
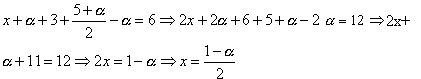
Assim, a solução do sistema é dada por S=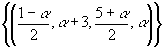 , com
, com 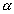
 IR.
IR.
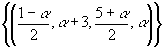 , com
, com
Para cada valor que seja atribuído a 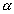 , encontraremos uma quádrupla que é solução para o sistema.
, encontraremos uma quádrupla que é solução para o sistema.
Nenhum comentário:
Postar um comentário